Knapsack problem

The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsackand must fill it with the most valuable items.

0/1 Knapsack Problem: Dynamic Programming Approach:

Knapsack Problem:

Knapsack is basically means bag. A bag of given capacity.

We want to pack n items in your luggage.

• The ith item is worth v_i dollars and weight w_i pounds.
• Take as valuable a load as possible, but cannot exceed W pounds.
• v_i w_i W are integers.

0/1 Knapsack Problem: Dynamic Programming Approach:

Knapsack Problem:

Knapsack is basically means bag. A bag of given capacity.

We want to pack n items in your luggage.

• The ith item is worth v_i dollars and weight w_i pounds.
• Take as valuable a load as possible, but cannot exceed W pounds.
• v_i w_i W are integers.

  0/1 Knapsack Problem: Dynamic Programming Approach:

  Knapsack Problem:

  Knapsack is basically means bag. A bag of given capacity.
  We want to pack n items in your luggage.
• The ith item is worth v_i dollars and weight w_i pounds.
• Take as valuable a load as possible, but cannot exceed W pounds.
• v_i w_i W are integers.

  0/1 Knapsack Problem: Dynamic Programming Approach:

  Knapsack Problem:

  Knapsack is basically means bag. A bag of given capacity.
  We want to pack n items in your luggage.
• The ith item is worth v_i dollars and weight w_i pounds.
• Take as valuable a load as possible, but cannot exceed W pounds.
• v_i w_i W are integers.

• Knapsack of capacity
• List (Array) of weight and their corresponding value.

Output: To maximize profit and minimize weight in capacity.

The knapsack problem where we have to pack the knapsack with maximum value in such a manner that the total weight of the items should not be greater than the capacity of the knapsack.

Knapsack problem can be further divided into two parts:

1. Fractional Knapsack: Fractional knapsack problem can be solved by Greedy Strategy where as 0 /1 problem is not.

It cannot be solved by Dynamic Programming Approach.

---

0/1 Knapsack Problem:

In this item cannot be broken which means thief should take the item as a whole or should leave it. That's why it is called 0/1 knapsack Problem.

• Each item is taken or not taken.
• Cannot take a fractional amount of an item taken or take an item more than once.
• It cannot be solved by the Greedy Approach because it is enable to fill the knapsack to capacity.
• Greedy Approach doesn't ensure an Optimal Solution.

---

Example of 0/1 Knapsack Problem:

Example: The maximum weight the knapsack can hold is W is 11. There are five items to choose from. Their weights and values are presented in the following table:

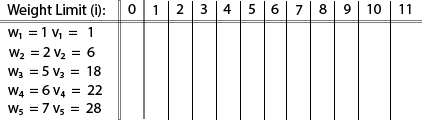
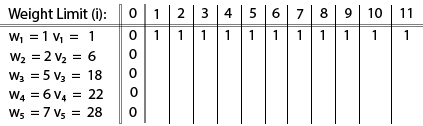
The [i, j] entry here will be V [i, j], the best value obtainable using the first "i" rows of items if the maximum capacity were j. We begin by initialization and first row.

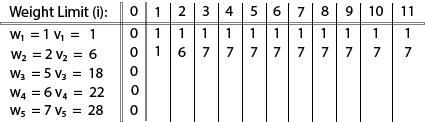
V [i, j] = max {V [i - 1, j], vi + V [i - 1, j -wi]

 

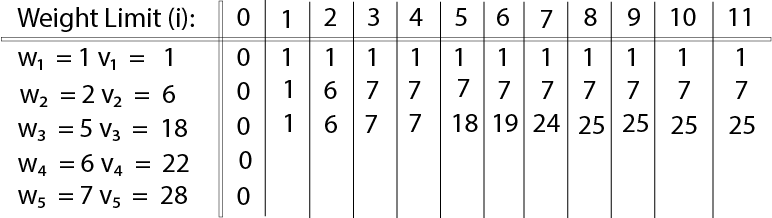
The value of V [3, 7] was computed as follows:

V [3, 7] = max {V [3 - 1, 7], v3 + V [3 - 1, 7 - w3]
         = max {V [2, 7], 18 + V [2, 7 - 5]} 
         = max {7, 18 + 6}
         = 24

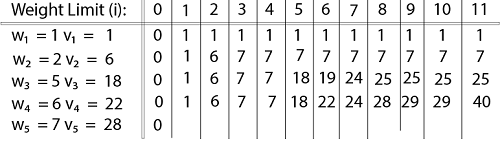
Finally, the output is:

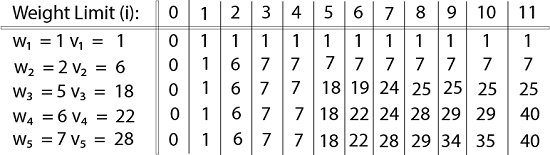
The maximum value of items in the knapsack is 40, the bottom-right entry). The dynamic programming approach can now be coded as the following algorithm:

---

Algorithm of Knapsack Problem

KNAPSACK (n, W)
 1. for w = 0, W
 2. do V [0,w] ← 0
 3. for i=0, n
 4. do V [i, 0] ← 0  
 5. for w = 0, W
 6. do if (wi≤ w & vi + V [i-1, w -  wi]> V [i -1,W])
 7. then V [i, W] ← vi + V [i - 1, w - wi]
 8. else V [i, W] ← V [i - 1, w]